
Neural Networks and Beyond
Overview
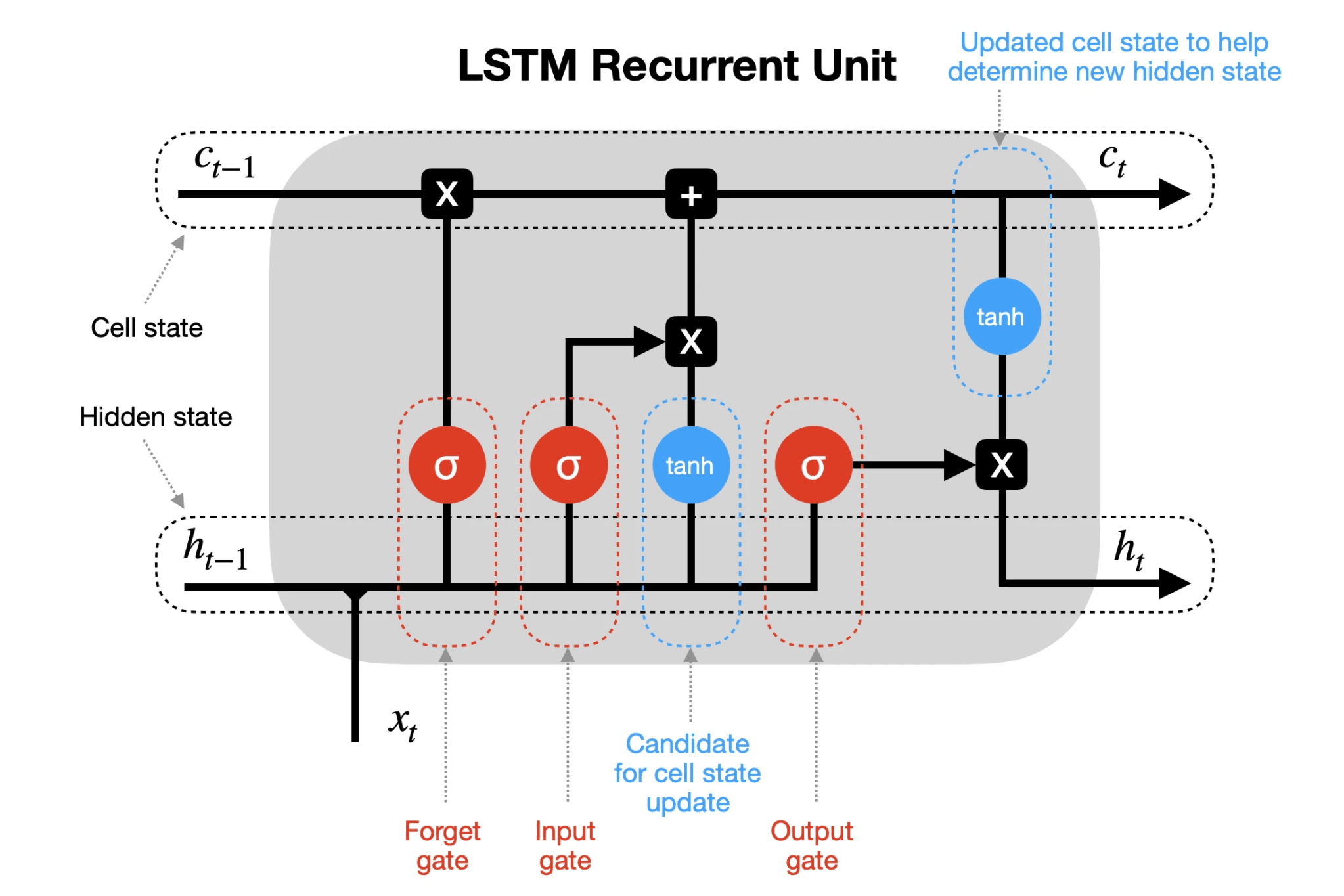
In this project, I built an end-to-end framework for continuous function approximation and symbolic regression by implementing linear, MLP, and custom LSTM architectures from scratch using NumPy and PyTorch. The models were trained to approximate nonlinear target functions and later distilled into interpretable symbolic forms using LASSO-based sparse regression.
For each stage, I:
Derived the mathematical foundations and forward/backward propagation equations
Implemented training using SGD and Adam optimizers from first principles
Visualized parameter trajectories, hidden activations, and low-dimensional manifolds (PCA)
Evaluated both numerical accuracy (low MSE) and symbolic interpretability of the approximated functions
This project provided an in-depth understanding of how neural networks internalize continuous mappings, bridging numerical learning with symbolic interpretability—demonstrating the fusion of deep learning and classical regression for transparent AI modeling.
Tools
Numpy
PyTorch
Semester
6
Grade
A+




Neural Networks and Beyond
Overview
In this project, I built an end-to-end framework for continuous function approximation and symbolic regression by implementing linear, MLP, and custom LSTM architectures from scratch using NumPy and PyTorch. The models were trained to approximate nonlinear target functions and later distilled into interpretable symbolic forms using LASSO-based sparse regression.
For each stage, I:
Derived the mathematical foundations and forward/backward propagation equations
Implemented training using SGD and Adam optimizers from first principles
Visualized parameter trajectories, hidden activations, and low-dimensional manifolds (PCA)
Evaluated both numerical accuracy (low MSE) and symbolic interpretability of the approximated functions
This project provided an in-depth understanding of how neural networks internalize continuous mappings, bridging numerical learning with symbolic interpretability—demonstrating the fusion of deep learning and classical regression for transparent AI modeling.
Tools
Numpy
PyTorch
Semester
6
Grade
A+

